Reset Windows Password v14.2
Telegram data recovery, Photo Database and Media Player investigation tools, and some more
Reset Windows Password v14.1
IP addresses history viewer, fast disk search, local security editor and some more
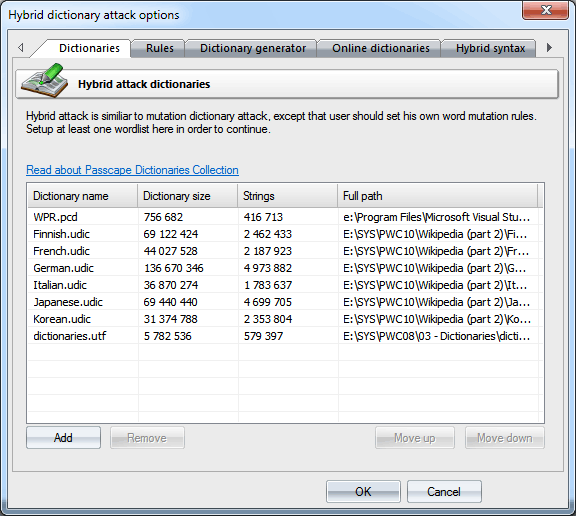
Windows Password Recovery - hybrid dictionary attack
Windows Password Recovery distribution kit comes with extended sets of password mutation rules:
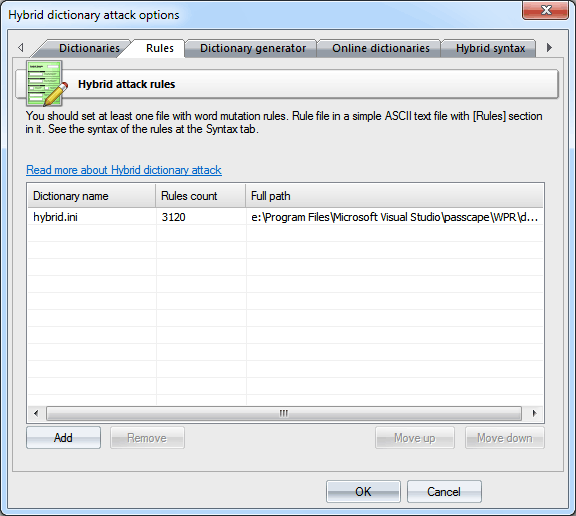
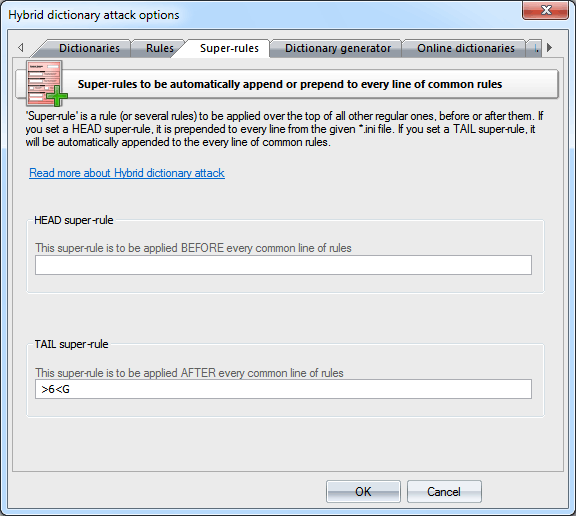
hybrid_rules/english_words.ini file contains basic rules for English passwords. hybrid_rules/nonenglish_words.ini holds common rules for non-Eglish passwords. hybrid_rules/simple_dates.ini - a lot of rules with dates, months, seasons, etc. hybrid_rules/l33t.ini - rules to freak words (based on the leet dictionary). For example, password->p@$$w0rd Read some additional info on rule efficiency in our blog DictionariesWordlists to be used in the attack are set on the first tab. Traditionally, the application supports wordlists in ASCII, UTF8, UNICODE, PCD, RAR and ZIP format. The position of the files on the list can be altered. For example, you may want to move smaller dictionaries up the list or the other way. During the attack, they will be used one after another, according to their position on the list. RulesOn the 'Rules' tab, define at least one file with password mutation rules. The format of the rules file is quite trivial; it is a plain-text ASCII file with the '[Rules]' string. Anything above this string is considered comments and ignored by the program. Whatever goes below this string is considered rules. Each string can contain several rules, applicable to a source word. The exclusion is the aN rule. This rule must not be on the same line with other rules. If a string contains multiple rules per word, those rules are parsed left to right. For example, if you apply the rule '@pc$a$b$c' to the source word 'password', at the output you will get 'Asswordabc'. The maximum length of an output word may not exceed 256 characters. Super-rulesSuper-rule is a rule (or several rules) to be applied over the top of all other regular ones, before or after them. For example, you can set 'a8' tail super-rule to create all possible case combinations after a common mutation has been done. So '/asa4' rule from l33t.ini file will become '/asa4a8', '/csc(' will become '/csc(a8', etc. Yet another one example: setting the '>6' head rule allows you to skip all words of less than 6 or greater than 16 characters, before starting a common mutation. This is a helpful feature once you decide to add the same rule to all text lines of the selected *.ini files. So there's no need to modify them all. Be careful though, the 'aN' super-rule may increase the total number of generated passwords drastically.
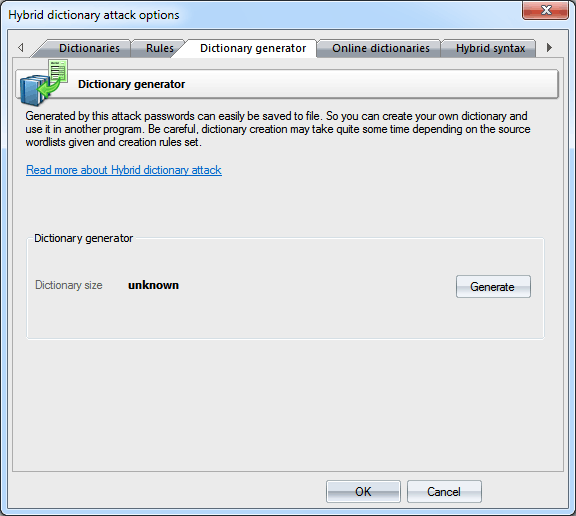
 Dictionary generatorThe Dictionary generator tab is designed for generating dictionaries obtained from an attack. Further on, those dictionaries could be used, for example, in other applications. To generate a dictionary, specify a source dictionary and a set of mutation rules for it. The size of a target file may exceed 2 GB. Be careful, the dictionary generation process may take considerable time!
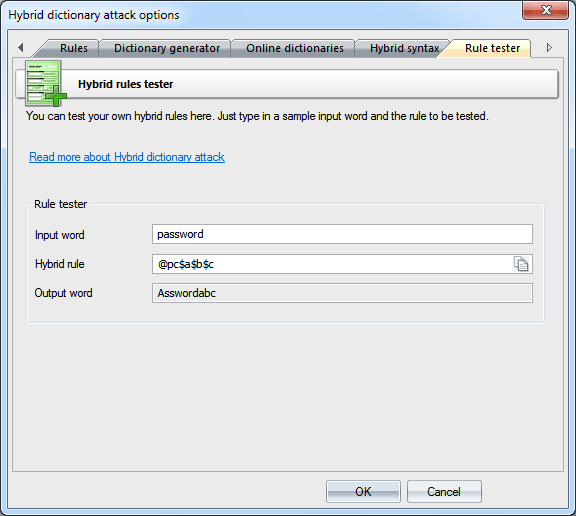
Online dictionariesYou can download additional wordlists for the attack using 'Online dictionaries' tab. SyntaxIf you want to create your own set of rules, you can use the last two tabs as sources of help. While the 'Syntax' tab gives mere descriptions of available rules, on the last tab you can actually test them by specifying a source word and a rule for the hybrid attack. Forward your rule sets to us; if we find them interesting/useful, we will include them in the default distribution of the program.
Rules description for the hybrid dictionary attack
loweralpha - abcdefghijklmnopqrstuvwxyz upperalpha - ABCDEFGHIJKLMNOPQRSTUVWXYZ alpha - abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ special - !@#$%^&*()-_+=~`[]{}|\:;"'<>,.?/ " loweralphanumeric - abcdefghijklmnopqrstuvwxyz0123456789 upperalphanumeric - ABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789 alphanumeric - abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789 printable - abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789!@#$%^&*()-_+=~`[]{}|\:;"'<>,.? / Feel free to forward your favorite rule files to us; if we find them interesting, we will include them in the default distribution of the program.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Rule | Example | Input | Output | Description |
| : | : | password | password | Do nothing to the input word. |
| { | { | password | asswordp | Rotate the word left. |
| } | } | password | dpasswor | Rotate right. |
| [ | [ | password | assword | Delete the first character. |
| ] | ] | password | passwor | Delete the last character. |
| c | c | password | Password | Capitalize. |
| C | C | password | pASSWORD | Anti-capitalize - lowercase the first character, uppercase the rest. |
| d | d | password | passwordpassword | Duplicate word. |
| f | f | password | passworddrowssap | Reflect word. |
| k | k | password пароль |
зфыыцщкв gfhjkm |
Convert word using alternative (first after default) keyboard layout. The rule works in both directions. For example, if there's Russian keyboard layout installed previously in the system, the rule should convert word 'password' to Russian 'зфыыцщкв', and Russian word 'пароль' to 'gfhjkm'. This is very helpful when looking for non-English passwords. If only one language is installed in the system, the rule does nothing. |
| K | K | password | passwodr | Swap last two characters. |
| l | l | PassWord | password | Convert all characters to lowercase. |
| q | q | password | ppaasssswwoorrdd | Duplicate all symbols in a word. |
| r | r | password | drowssap | Reverse word. |
| t | t | PassWord | pASSwORD | Toggle case of all characters |
| u | u | password | PASSWORD | Convert to uppercase. |
| U | U | my own password | My Own Password | Capitalize all words delimited with space (upper-case the first character and every character after space). |
| V | V | password | PaSSWoRD | Vowels elite. |
| v | v | password | pASSWoRD | Vowels noelite. |
| 'N | '4 | password | pass | Truncate the word to N character(s) length. |
| +N | +1 | password | pbssword | Increment character at position N by 1 ASCII value. |
| -N | -0 | password | obssword | Decrement character at position N by 1. |
| .N | .4 | password | passoord | Replace character at position N with character at position N+1 |
| ,N | ,1 | password | ppssword | Replace character at position N with character at position N-1. Where N > 0. |
| Reject (skip) the word if it is greater than N characters long. | ||||
| >N | Reject (skip) the word if it is less than N characters long. | |||
| _N | _8 | Reject (skip) the word if it's length is not N. | ||
| aN | a8 | Check all possible symbol cases for the word. N is a maximal length of the word to apply this rule for. | ||
| DN | D2D2 | password | paword | Delete the character at position N. |
| pN | p3 | key | keykeykey | Copy word N times. |
| SLN | SL2 | 012345678 | 01d345678 | Bitwise shift left character at position N. |
| SRN | SR2 | password | pa9sword | Bitwise shift right character at position N. |
| TN | T1T5 | password | pAsswOrd | Toggle case of the character at position N. |
| yN | y3 | password | paspasword | Duplicate first N characters. |
| YN | Y3 | password | paswordord | Duplicate last N characters. |
| zN | z3 | password | ppppassword | Duplicate the first character of the word N times. |
| ZN | Z3 | password | passwordddd | Duplicate the last character of the word N times. |
| $X | $0$0$7 | password | password007 | Add character X to the end of the word. |
| ^X | ^3^2^1 | password | 123password | Insert character X at the beginning of the word. |
| @X | @s | password | paword | Remove all characters X from the word. |
| !X | !. | Reject (skip) the word if it contains at least one character X. | ||
| /X | /1/2/3 | Reject (skip) the word if it does not contain character X. | ||
| (X | (p | Reject (skip) the word if the first character is not X. | ||
| )X | )d | Reject (skip) the word if the last character is not X. | ||
| eX | e@ | mike@yahoo.com | mike | Extract a substring starting at position 0 and ending up before the first occurrence of X character (do nothing if X is not found). |
| EX | E@e. | mike@yahoo.com | yahoo | Extract a substring starting right after first found X character and till the end of the string (do nothing if X is not found). |
| %MX | %20 | Reject (skip) the word if it does not contain at least M instances of the character X. | ||
| *XY | *15 | password | possward | Swap characters at positions X and Y. |
| =NX | =01 | Reject (skip) the word if the character at position N is not equal to the X | ||
| iNX | i4ai5bi6c | password | passabcword | Insert the character X in position N. |
| oNX | o4*o5* | password | pass**rd | Overwrite a character in position N with the character X. |
| sXY | ss$so0 | password | pa$$w0rd | Replace all characters X with Y. |
| xNM | x4Z | password | word | Extract a substring of up to M characters length, starting from position N. |
| INX-Y | rI0/-/r | google.com | google.com/ | Insert the character X at position N if the previous character at position N is not Y. |
| INX+Y | rI0.+.r | password. | password.. | Insert the character X at position N if the previous character at position N is Y. |
| ONX-Y | O0-+p | password | -assword | If the character at position N is not Y, overwrite it with X character. |
| ONX+Y | O0P+p | password | Password | If the character at position N is Y, overwrite it with X character. |
| RNM+Y | R01+a | password | assword | Remove character at position N if the character at position M is Y |
| RNM-Y | R40-b | password | passord | Remove character at position N if the character at position M is not Y |
| ?iN[C] | ?i0[digits] | password | 0password .. 9password |
Insert a character from a charset [C] into position N of the word. Where C should be either a predefined charset name or a custom character set itself. |
| ?iZ[C] | ?iZ[digits] | password | password0 .. password9 |
Insert a character from a charset [C] into the last position of the input word. |
| ?i[C] | ?i[special] | password | ~password .. password+ |
Insert a character from a charset [C] into every position of the word. [C] should be either a predefined charset name or a custom character set itself. |
| ?oN[C] | ?o1[upperalpha] | password | pAssword .. pZssword |
Overwrite a character at position N with a character taken from the charset [C]. Where C should be either a predefined charset name or a custom character set itself. |
| ?oZ[C] | ?oZ[upperalpha] | password | passworA .. passworZ |
Overwrite a character at the last position with a character taken from the charset [C]. |
| ?o[C] | ?o[-=.] | password | -assword .. password. |
Overwrite a character at every position of the word with a character taken from a charset [C]. Where C should be either a predefined charset name or a custom character set itself. The given example (?o[C] rule for the word password) will generate the following combinations: -password, =password, .password, -assword, =asswords, .assword, p-ssword, p=ssword ... password. |