Base-word attack

Base-word attack (developed by Passcape) is an irreplaceable recovery tool when you know a portion of the password or its basic component. Normally, such cases dispose to using mask attack; however, it does not always allow coping with the task set forth. Suppose our password was 'S10wDr1v3r'. Trying to recover such a complicated password using brute-force attack would be an ungrateful job, even if you are quite sure that it is based upon the 'slowdriver' word. These are the cases when the base-word attack will rescue you.

With this tool, the program will attempt to recover the original password, trying all possible combinations founded upon 15 groups of rules (total over 150 rules.) If you enter 'slowdriver' in the field, you will see that the program has generated several thousands of different combinations upon this phrase, and one of those combinations could match our password.
 

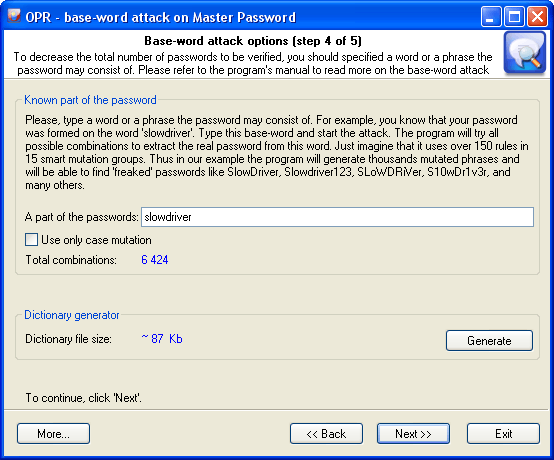
If the length of the phrase exceeds 8-10 characters, the mutation may take significant time. If you remember the original password precisely and simply have forgotten the sequence of the upper-case and lower-case characters in it, you can select the option 'Use only case mutations'. With this option selected, the program will generate passwords with all possible combinations of upper-case and lower-case characters, total 2^n passwords, where n - is password length. For example, for the password 'slowdriver' the program will generate 2^10=1024 different combinations for each keyboard layout installed on your computer.